Python Transpose Numpy Function [4 Code Examples]

In this article, we’ll learn about the Python transpose Numpy function. We’ll explore the parameters of this function. To make this article interesting, we’ll apply the transpose function to 1D and 2D arrays and understand the implementation with proper code examples.

What is Python Transpose Numpy Function?

If you want to rearrange the dimensions of an array, then use the transpose() function. It can reverse the order which means the swapping of array dimensions. This function is very good for transformations of data, reshaping data to generate calculations that are much more efficient, or matrix operations.

Syntax

numpy.transpose(array, axes=None)

Parameters

• The first parameter is actually an array. That array will be used for transposition.
• The second parameter ‘axes‘ is used to guide the function of which dimensions order we want to create. Or in simple words, we can say that it defines the new order of dimensions. This parameter is optional and not specifying it or providing it the ‘None‘ value will by default reverse the dimension’s order.

4 Examples of implementing the transpose() function

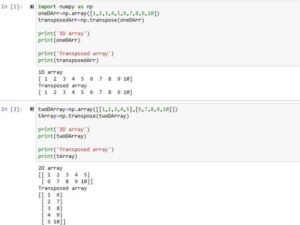
Example 1: transpose function applied on a 1D array

import numpy as np
oneDArr=np.array([1,2,3,4,5,6,7,8,9,10])

transposedArr=np.transpose(oneDArr)   # transposing occurs here

print('1D array')
print(oneDArr)

print('Transposed array')
print(transposedArr)

Output

1D array
[ 1  2  3  4  5  6  7  8  9 10]
Transposed array
[ 1  2  3  4  5  6  7  8  9 10]

In this code example:

1. We have first imported the numpy library so we can use its transpose() function and also for creating an array.
2. At first, we created a simple 1D array and store it inside a variable.
3. Then we applied the transpose function on it by passing that 1D array as an argument to this function.
4. Finally, we printed the value of both the 1D array and transposed array.
5. The output is the same for both arrays. The reason is that the transposed of a one-D array is itself because of one dimension that it has.

Example 2: Apply transpose() on 2D Array

twoDArray=np.array([[1,2,3,4,5],[6,7,8,9,10]])

tArray=np.transpose(twoDArray)     # applying transpose

print('2D array')
print(twoDArray)

print('Transposed array')
print(tArray)

Output

2D array
[[ 1  2  3  4  5]
 [ 6  7  8  9 10]]
Transposed array
[[ 1  6]
 [ 2  7]
 [ 3  8]
 [ 4  9]
 [ 5 10]]

In this code example, we’ve transposed the 2D array using the transpose() numpy function. We can see that the rows and columns are being flipped and swap the position of elements along the main diagonal. The difference can be seen in the above output section where we displayed the 2D array and the transposed array.

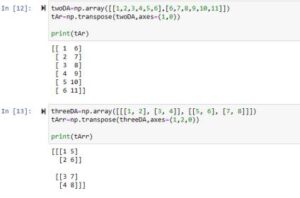
Example 3: Parameter ‘axes‘ of transpose()

twoDA=np.array([[1,2,3,4,5,6],[6,7,8,9,10,11]])

tAr=np.transpose(twoDA,axes=(1,0))  # axes parameter customized

print(tAr)

Output

[[ 1  6]
 [ 2  7]
 [ 3  8]
 [ 4  9]
 [ 5 10]
 [ 6 11]]

In this code, we passed the axes parameter (1,0). It specifies the (axis 1) first dimension becomes the second dimension while the (axis 0) second dimension becomes the first dimension. The output can be seen above and it shows pretty much the same result as generated in example 2. The reason is that 2D array transposing is similar to swapping its axis.

Example 4: 3D array with axes (1, 2, 0)

threeDA=np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])

tArr=np.transpose(threeDA,axes=(1,2,0))

print(tArr)

Output

[[[1 5]
  [2 6]]

 [[3 7]
  [4 8]]]